An important point in the credibility revolution, ironically, was the 1970s empirical crisis in labor economics. It wasn’t the sort we find today; not exactly. It wasn’t a problem of data fabrication, coding errors or p-hacking. Rather, it was a crisis in empirical labor and empirical macro studies where many studies were viewed and believed, in an epistemological sense, to be flawed or lacking credibility. They weren’t flawed because the data were flawed. They weren’t flawed because the questions were flawed. And they weren’t flawed because the underlying econometric models were themselves flawed. They were driven mostly by human error which is a little difficult to explain. But perhaps no other study done at that time exemplifies the flaws of the studies in question, at least in labor economics, that Robert LaLonde’s 1986 article.
Yesterday, I found a new working paper by Guido Imbens and Yiqing Xu, both professors at Stanford. Imbens, are readers know, is the 2021 co-recipient of the Nobel Prize in economics, and Xu is an assistant professor in the political science department as well as a contributor to a range of studies, including ones in statistical methodologies using causal panel data. He is also an excellent creator of statistical software, such as R’s -gsynth- package which is home to several causal panel methods (including matrix completion with nuclear norm regularization), and makes beautiful repositories for his work. This new working paper is entitled “LaLonde (1986) after Nearly Four Decades: Lessons Learned” and for those who, like me, are enthusiastic consumers of the history of design based causal inference, I encourage you to read it, as you likely already know that LaLonde’s paper was pivotal, at least in hindsight.
Who was Bob Lalonde and what was his 1986 study?
Last November, I wrote a short substack about Robert LaLonde and that now famous job market paper of his. You can find the substack here.
The name of the article, published in the flagship journal American Economic Review, was “Evaluating the Econometric Evaluations of Training Programs with Experimental Data”. The context was the evaluation of job trainings programs, which seemed to be a popular topic in program evaluation and applied labor economics in the 1970s and through the 1990s. Many people wrote on it, including Ashenfelter, Heckman, Card, and then not to mention the many applied researchers at research corporations like MDRC. The job training program in question was the National Support Work Demonstration or NSW and I discuss the details of the intervention here in my book here in this section in section 5.3.4 “Example: The NSW job training program”.
The study has two parts:
Evaluate an RCT conducted by MDRC involving a job trainings program on real earnings. The experimental average effect of the program was found to be around $800-900 for males and females, analyzed separately.
Drop the experimental control group and replace it with several comparison groups drawn broadly from the US population (e.g., CPS, PSID), then using contemporary micro econometric methods, see if he can “recover” the known average effect of $800-900.
LaLonde’s analysis of the experimental treatment group matched with various non-experimental control groups found a range of estimates, many of the wrong sign, and almost none which were close to the experimental effect.
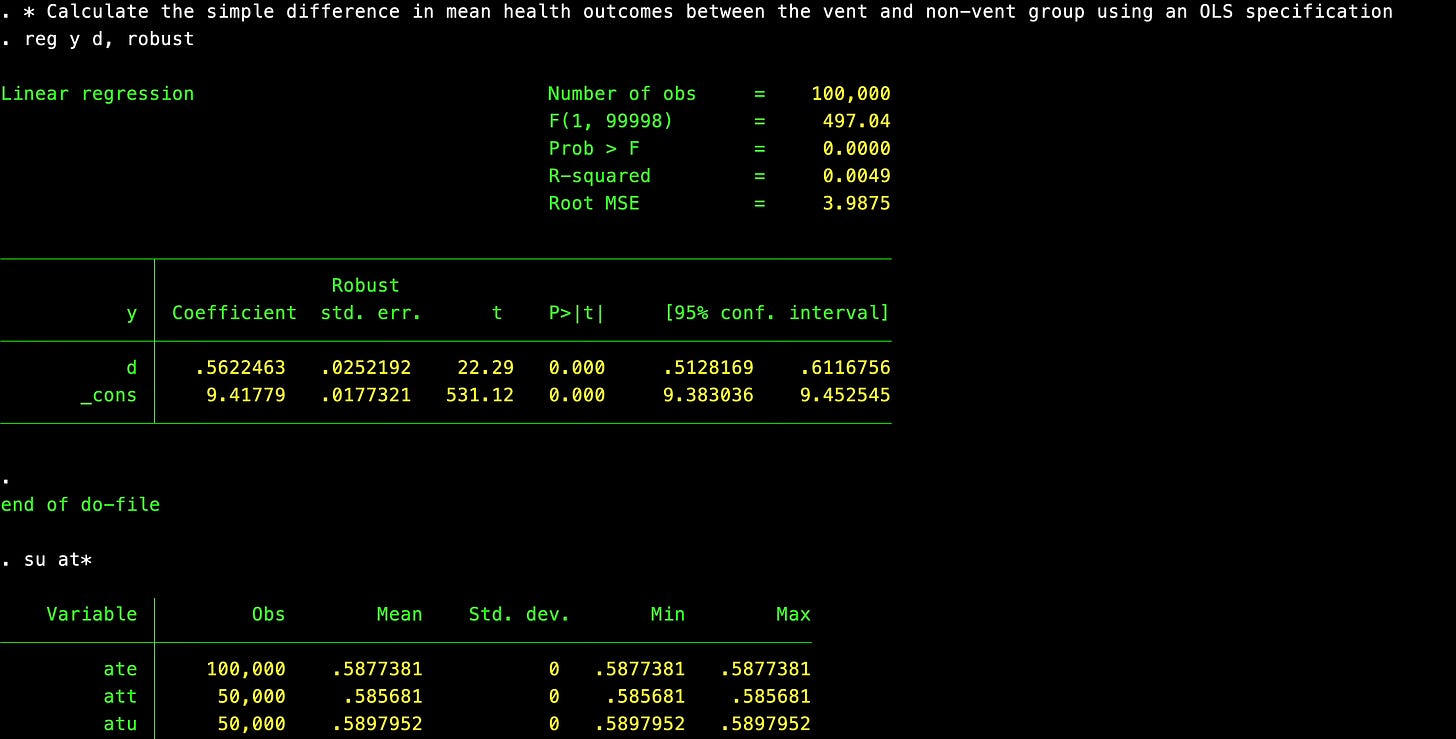
It’s worth saying, first, that in an RCT, the ATE and the ATT are the same number. You can see this by working out the implications of the independence assumption when applied to a simple difference in mean outcomes. The simple difference in mean outcomes will show that the ATE and the ATT and the ATU for the matter are the same number. Here’s code to illustrate it and output.
| ***************************************************** | |
| * name: perfect_doctor.do | |
| * author: scott cunningham (baylor) | |
| * description: simulation of a perfect doctor assigning the treatment | |
| ***************************************************** | |
| clear | |
| capture log close | |
| set seed 20200403 | |
| * 100,000 people with differing levels of covid symptoms | |
| set obs 100000 | |
| gen person = _n | |
| * Potential outcomes (Y0): life-span if no vent | |
| gen y0 = rnormal(9.4,4) | |
| replace y0 = 0 if y0<0 | |
| * Potential outcomes (Y1): life-span if assigned to vents | |
| gen y1 = rnormal(10,4) | |
| replace y1 = 0 if y1<0 | |
| * Define individual treatment effect | |
| gen delta = y1-y0 | |
| * Bad doctor assigns vents to first 50,000 ppl and no vents to second 50,000 ppl | |
| gen d = 0 | |
| replace d = 1 in 1/50000 | |
| * Calculate all aggregate Causal Parameters (ATE, ATT, ATU) | |
| egen ate = mean(delta) | |
| egen att = mean(delta) if d==1 | |
| egen atu = mean(delta) if d==0 | |
| egen att_max = max(att) | |
| egen atu_max = max(atu) | |
| * Use the switching equation to select realized outcomes from potential outcomes based on treatment assignment given by the Bad Doctor | |
| gen y = d*y1 + (1-d)*y0 | |
| * Calculate EY0 for vent group and no vent group (separately) | |
| egen ey0_vent = mean(y0) if d==1 | |
| egen ey01 = max(ey0_vent) | |
| egen ey0_novent = mean(y0) if d==0 | |
| egen ey00 = max(ey0_novent) | |
| * Calculate selection bias based on the previous conditional expectations | |
| gen selection_bias = ey01-ey00 | |
| * Calculate the share of units treated with vents (pi) | |
| egen pi = mean(d) | |
| * Manually calculate the simple difference in mean health outcomes between the vent and non-vent group | |
| egen ey_vent = mean(y) if d==1 | |
| egen ey1 = max(ey_vent) | |
| egen ey_novent = mean(y) if d==0 | |
| egen ey0 = max(ey_novent) | |
| gen sdo = ey1 - ey0 | |
| * Calculate the simple difference in mean health outcomes between the vent and non-vent group using an OLS specification | |
| reg y d, robust |
As you can see in the simulation, the ATE and ATT under this randomized treatment assignment are roughly 0.59 and the estimated coefficient is 0.56.
So back to LaLonde. LaLonde’s original estimate using the RCT data was around $800-900. When LaLonde drops the experimental control group, and replaces it with the non-experimental control group, the ATE will no longer by $800-900 as the ATE is the average treatment effect for the entire population and now the entire population (in the data mind you) has changed. But the ATT should be the same, as remember, the ATE and the ATT are the same in the trial, so when you keep the experimental treatment group and estimate only the counterfactual for them, it should be the ATT.
LaLonde’s original paper, as Imbens and Xu say here, tends to “de-emphasize heterogeneity” and therefore some of his specifications are not designed to estimate the ATT making evaluation of his results as necessarily contradicting the RCT finding a little difficult. Most likely the ATE in the matched sample of 297 treated units (experimental) and sometimes 16,000 comparison units drawn from a random sample of Americans (though as Imbens and Xu note, he used selection criteria to make the different datasets “more comparable”) is negative to be honest. Most people in America are very different from the select sample of people enrolled in the NSW as the NSW consisted of extremely disadvantaged groups. Women were drawn from AFDC. Men were typically ex-convicts, people with substance abuse disorders, and in terms of income, are clearly from the far left tail of the income distribution compared the non-experimental controls. But, the ATT should still be $800-900.
The overall conclusion of the 1986 study, though, was pessimism given he was unable to recover in a reasonable specification that one would’ve chosen ex ante (and he tries a lot of them) close to that number. He concludes, like his professors before him Ashenfelter and Card, for more explicit randomization of job trainings programs, and by extension, many interventions. And that is not really what people remember about the LaLonde study — that the pessimism over program evaluation using non-experimental data was so extreme that he (and others at Princeton) suggested economists going forward should not just consider, but in fact should push for, explicit randomization for evaluation purposes. In today’s minds, this is not radical, but in empirical labor at the time, that was quite radical. It was rare to see such RCTs, which is hard to really put yourself in the mindset of given the average JMP in development will be a large field RCT, and increasingly, many outside of development as well.
Where are they now?
The paper does a follow up. A kind of “where are they now?” post-script like we long for at the end of a biopic. Where are the characters in the story from the 1970s now, 50 years later? Are they doing okay? Did they achieve their dreams? And I think you can say from reading Imbens and Xu that while the original LaLonde conclusions has some merit, we still have some reasons to be optimistic about non-experimental studies — at least when done well.
The underlying statistical methodology that Imbens and Xu emphasize throughout the paper is that of unconfoundedness. That is, conditional on covariates, the treatment is based on a treatment assignment mechanism wherein people were put into the treatment for reasons that were unrelated to their potential outcomes, including the gains to the treatment.
Pause for a moment — human beings do not ordinarily produce data that “unconfoundedness”. At least, economists don’t think so, and I wrote an old substack about this called “Why Do Economists So Dislike Conditional Independence?” If you’re interested, you can read it here.
The reason why in a nutshell economists “so dislike conditional independence” can be divided into two more or less identical reasons, but probably which are two different perspectives. The first perspective is a kind of “hands thrown up in despair” reason which is that most economists no longer know the variables to include even in principle because most economists do not use economic models to aid in setting up the natural experiment. David Card talks about this in his Nobel prize speech and in an old speech he gave regarding empirical micro moving away from models and towards “design” (gated, ungated). As you move away from models, you move away from things akin to graphical models like Pearl’s DAGs, and without those, selection of covariates satisfying unconfoundedness is borderline impossible. A great paper is by Carlos Cinelli, et al. entitled “A Crash Course in Good and Bad Controls”. So that’s one reason — as we move away from models, we move away from methods that will help us select covariates. So the kind of movements Card describes likely also made unconfoundedness based methodologies a challenge to say the least.
But a second reason I emphasize in my essay is a criticism based on economist’s one model, and that one model is “rational choice”. It is hard wired into the mother boards of the modal economists that humans maximize utility subject to budget constraints, firms maximize profits, minimize costs, and governments maximize something. Maximization and minimization almost certainly violates unconfoundedness because both use target quantities as objective functions like “gains from a choice”, and gains from a choice mean Y(1)-Y(0)>0. Take the action, in other words, if and only if the gains are positive, other wise do not. Heckman often points to this in Roy’s early work and calls it the Roy model and it describes sorting patterns based on gains. Unconfoundedness does not deny such sorting, but rather says the sorting “selects” on covariates such that when you control for those covariates, all remaining choices human makes are coin flips. But I think this still is not appetizing to economists when they really understand what unconfoundedness. They may find it acceptable to run regressions “controlling for stuff” because they’re so used to thinking of endogeneity in terms of “omitted variable bias”, but if you tell them that endogeneity also means that observationally equivalent groups of people select into some treatment by random chance (i.e., coin flips), I think they balk, and rightfully so. We weren’t run over the coals that first year of PhD microeconomics just to punt on rational choice so we can run a regression.
Keep reading with a 7-day free trial
Subscribe to Scott's Mixtape Substack to keep reading this post and get 7 days of free access to the full post archives.